ГЕНЕРАТОР РАСПОЗНАВАТЕЛЕЙ UNISAN

А. И. Толкачёв (tolkachyov@gsu.by),

М. С. Долинский (dolinsky@gsu.by)

Гомельский государственный университет им. Ф. Скорины (Гомель, Беларусь)

В статье описаны алгоритмы, положенные в основу генератора распознавателей Unisan, разработанного и успешно применяемого в Гомельском государственном университете. Рассматривается представление распознавателя в виде множества синтаксических диаграмм, алгоритм построения распознавателя по РБНФ – описанию грамматики, алгоритм построения SLL¹(k) распознавателя, эвристический алгоритм факторизации синтаксических диаграмм, позволяющий в ряде случаев привести грамматику к виду SLL¹(k). Все алгоритмы описаны с учётом возможности наличия в грамматике символов действия. Приводятся результаты сравнения по основным характеристикам Unisan с широко используемыми генераторами распознавателей.

1. ВВЕДЕНИЕ

Необходимость обработки текстовой информации, вводимой человеком, возникает в самых разнообразных программных продуктах – от компьютерных игр до компиляторов. В большинстве случаев эта обработка осуществляется с использованием лексического и синтаксического анализаторов [1-3].

Поскольку написание лексического и синтаксического анализаторов на каком-либо алгоритмическом языке программирования – весьма трудоёмкий процесс и внутренняя структура анализаторов практически не зависит от синтаксиса обрабатываемого языка, то для построения анализаторов используются т.н. генераторы распознавателей.

Генератор распознавателей представляет собой универсальное программное обеспечение, позволяющее по заданному формальному описанию некоторого языка автоматически получить для него лексический и синтаксический анализаторы.

Основные требования, предъявляемые подобным систем – простота и наглядность формального описания грамматики, эффективность по скорости работы и требуемому объёму памяти как анализатора, так и генератора распознавателей, возможность использования системы в проектах, разрабатываемых с использованием различных языков программирования. Из конкретных применений генераторов распознавателей можно выделить создание инструментария для разработки программного обеспечения встроенных систем, быстро развивающихся в последнее время. При создании или настройке компиляторов, интерпретаторов или ассемблеров для таких систем непременно возникает необходимость изменения синтаксиса входного языка при переходе с одной платформы на другую (добавление специфических ключевых слов, типов данных и др.). По этой причине класс грамматик, поддерживаемый генератором распознавателей, должен быть достаточно широким для того, что бы внесение изменений в описание грамматики не требовало значительных усилий со стороны программиста.

Многие существующие программные средства не удовлетворяют перечисленным требованиям. Актуальной является и теоретическая разработка проблемы, поскольку методы, известные в теории грамматик, часто оказываются неприменимыми или недостаточно эффективными для задач, возникающих на практике. Об актуальности проблемы свидетельствует и появление новых работ [4-7], касающихся теории грамматик.

В данной статье описывается алгоритм построения распознавателя, реализованный в программном комплексе Unisan. Распознаватель позволяет работать с SLL¹(k), k ³ 1 - грамматиками [4, 5], которые являются подмножеством LL(k) [1]. Объём памяти и время, необходимое для распознавания и построения распознавателя для SLL¹(k) – грамматики, линейно зависит от k, что позволяет эффективно использовать грамматики при k>1. Кроме этого, используется эвристический алгоритм факторизации синтаксических диаграмм, позволяющий в ряде случаев уменьшить k или даже привести грамматику к виду SLL¹(k), если она не являлась такой в исходном виде. Из дополнительных возможностей отметим наличие механизма, позволяющего управлять потоком лексем во время разбора. Эта возможность упрощает реализацию, например, макроподстановок или включения файла в исходный текст (директива #include препроцессора языка С). ПТК Unisan реализован на языке C++. На данный момент имеется версия для платформы Win32, хотя, при необходимости, возможно его портирование на другие платформы.

В пунктах 2-5 вводятся необходимые определения и описывается способ представления грамматики и распознавателя, в пунктах 6-7 описан используемый алгоритм построения SLL¹(k) – распознавателя, в пункте 8 – алгоритм факторизации синтаксических диаграмм.

2. ТЕРМИНОЛОГИЯ

Алфавит - произвольное конечное множество, элементы которого будем называть символами.

Множество Â(M) - множество всех подмножеств множества M.

Бинарное отношение на множестве M – произвольное подмножество множества M ´ M. Мы будем использовать только бинарные отношения, поэтому будем называть бинарное отношение просто отношением.

Ориентированным графом назовём двойку Г=(S,R), где S – конечное множество вершин, R – отношение на множестве S. Элемент (s₁,s₂)ÎR называется ребром или дугой графа, ведущей из вершины s₁ в вершину s₂.

Ориентированный граф Г=(S,R) будем называть помеченным, если определена функция разметки c, отображающая элементы S È R в некоторое множество. Будем говорить, что символ a приписан дуге (или ребру) b, если aÎc(b).

Графически вершины графа будем изображать кругами, дуги – стрелками, соединяющими круги так, что если (s₁,s₂)ÎR, то проведена стрелка из круга s₁ в круг s₂. Если определена функция разметки, отображающая вершину или дугу в некоторое множество A, рядом с этой вершиной или дугой будем изображать соответствующий элемент множества A.

Строка (цепочка) символов – конечная упорядоченная последовательность символов алфавита. Пустую строку будем обозначать e.

Если a = a₁ … a_n и b = b₁ … b_m – цепочки, то ab = a₁ …a_n b₁ … b_m – цепочка, называемая конкатенацией цепочек a и b.

Символом, возведённым в степень n, будем обозначать строку из n символов. Например, a³ – строка ‘aaa’, T² – строка из двух символов алфавита T.

Строка с нижним индексом i – i-й символ строки, например, (abcd)₃ = c.

Мощность множества M будем обозначать |M|, |a| - длина цепочки a, т.е. количество символов в ней.

Пусть abg - цепочка. a назовём префиксом цепочки abg, g - суффиксом цепочки abg.

k-префиксом цепочки a назовём цепочку a_1…k:

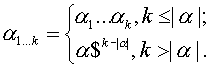
Символ $ ниже будет использоваться как маркер конца строки.

Множество всех строк (включая пустую), которые могут быть построены из символов алфавита T, называется замыканием T и обозначается T^*. Положительное замыкание T (обозначается T⁺) - множество T^*\{e}, т.е. множество всех строк, которые могут быть построены из символов алфавита T, за исключением пустой строки.

Язык в алфавите T – подмножество множества T^*.

Контекстно-свободная грамматика – пятёрка G( N, T, A, P, S ), где

· N – алфавит нетерминальных символов (нетерминалов), (1)

· T – алфавит терминальных символов (терминалов),

· A – алфавит символов действия (СД),

· PÍ N ´ ( N È T )^* – конечное множество правил (продукций) грамматики,

правила будем записывать в виде B à a, где a Î (N È T È A)^*, B Î N,

· SÎN – главный нетерминал грамматики (аксиома грамматики).

Алфавитом грамматики называется множество N È T È A.

Словом, начинающимся с ‘$’, будем обозначать символ, используемый в специальных целях ($PUSH, $POP, $). Предполагается, что такие символы не входят во множества N, T, A.

Заметим, что в классическом определении грамматики [1] отсутствует множество символов действия A. Мы будем рассматривать СД наравне с нетерминалами и терминалами. Символы действия не влияют на синтаксис языка, но служат для придания ему семантики. Распознаватель, ‘проходя’ через каждый СД, вызывает определённую процедуру. Ниже будет пояснён механизм работы распознавателя с СД.

Если не указано иначе, строки символов алфавита грамматики будем обозначать маленькими греческими буквами a, b, …

Множество выводимых цепочек грамматики G определим следующим образом:

1) S – выводимая цепочка.

2) Если abg - выводимая цепочка и b à d содержится в P, то adg - выводимая цепочка.

Выводимая цепочка грамматики G, не содержащая нетерминальных символов, называется терминальной цепочкой, порождённой грамматикой G. Заметим, что терминальная цепочка может содержать СД.

Язык, порождаемый грамматикой G (обозначается L(G)), - это множество терминальных цепочек, порождаемых грамматикой G.

Пусть G(N,T,A,P,S) – грамматика. Определим отношение Þ_G на множестве (N È T È A)^*: если abg - цепочка из (N È T È A)^* и bàd Î P, то abgÞ_G adg (adg непосредственно выводима из abg). Транзитивное замыкание отношения ÞG обозначим Þ_G⁺ (adg выводима из abg за один или более шагов), рефлексивное замыкание - Þ_G^* (adg выводима из abg). Если понятно, о какой грамматике идёт речь, нижний индекс G будем опускать.

Конечным автоматом над алфавитом T называется шестёрка K=(S, T, d, s₀, Q, m), где

· S – конечное множество состояний;

· T – конечное множество допустимых входных символов;

· d - отображение множества S ´ T в множество Â(S) \ {Æ}, d называется функцией переходов;

· s₀ÎS – начальное состояние;

· Q – конечное множество маркеров;

· m - отображение множества Q в множество Â(S), m для каждого маркера указывает множество состояний, помеченных этим маркером. Обратное отображение будем обозначать m^-1 – отображение множества S в множество Â(Q), для каждого состояния sÎS указывает множество маркеров, которыми оно помечено.

Конечный автомат K назовём детерминированным, если "(q,t)ÎQ´T |d(q,t)|=1. В противном случае конечный автомат будем называть недетерминированным.

Конфигурацией конечного автомата назовём двойку (s, t), где sÎS, tÎT^*.

Такт работы конечного автомата K определим как отношение ®_K на его конфигурациях: (s,tt)®_K(s’, t), если s’Îd(s,t). Транзитивное и рефлексивное замыкание ®_K будем обозначать ®^*_K. Если из контекста понятно, о каком автомате K идёт речь, то будем опускать нижний индекс K в обозначении ®_K.

Состояние sÎS конечного автомата называется недостижимым, если не $t,wÎT^*, (s0, tw)®^*(s,w).

Графически конечный автомат изображается в виде диаграммы состояний. Диаграмма состояний – ориентированный граф Г=(S, R_Г), вершинами которого являются состояния автомата, множество дуг и функция разметки c строятся по следующему правилу: если s₂Îd(s₁,t), то (s1,s2)ÎR_Г, tÎc(s1,s2), если sÎS, то c(s)={q | sÎm(q)}. Вершина $ERRORÎS и дуги, ведущие в неё, не изображаются.

3. ОПИСАНИЕ ПРАВИЛ ГРАММАТИКИ С ПОМОЩЬЮ РБНФ

РБНФ (расширенная БНФ, форма Бэкуса-Наура, нормальная форма Бэкуса) является общепринятым способом описания формальных грамматик.

Пример описания грамматики с помощью РБНФ:

A à число ^сохранить_прочитанное_число *(B)

B à ‘+’ число ^сложить_прочитанное_число_с_предыдущим_и_сохранить_результат

В приведённом примере N = {A, B}, T = {число}, A = {сохранить_прочитанное_число, сложить_прочитанное_число_с_предыдущим_и_сохранить_результат}.

Выражение, стоящее справа от символа à, будем называть правой частью правила. Правая часть правила РБНФ является регулярным выражением над алфавитом N È T È A.

Множество регулярных выражений над алфавитом X обозначим REG(X). Регулярное выражение rÎREG(X) порождает некоторое множество цепочек символов алфавита X. Множество REG(X) и порождаемые его элементами цепочки определим следующим образом:

· a Î REG(X) "a Î X. Выражение a порождает цепочку, состоящую из одного символа a;

· если a Î REG(X), b Î REG(X), то a b Î REG(X). Выражение a b порождает множество цепочек, получаемых конкатенацией некоторой цепочки, порождаемой выражением a и некоторой цепочки, порождаемой b. Для обозначения конкатенации a b будем также использовать выражение a . b;

· если a Î REG(X), b Î REG(X), то (a | b)Î REG(X). Выражение (a | b) порождает объединение множеств цепочек, описываемых a и b;

· если a Î REG(X), то *(a) Î REG(X). Выражение *(a) называется итерацией a и порождает множество цепочек, являющихся конкатенацией произвольного (нулевого или положительного) количества цепочек, порождаемых выражением a;

· если a Î REG(X), то +(a) Î REG(X). Выражение +(a) называется положительной итерацией a. Положительная итерация a отличается от итерации a тем, что порождает конкатенацию положительного числа цепочек;

· если a Î REG(X), то ?(a) Î REG(X). Выражение ?(a) порождает все цепочки, порождаемые выражением a, а так же пустую цепочку (т.е. цепочку нулевой длины).

При использовании правил РБНФ для описания грамматики необходимо переопределить отношение Þ_G: если abg - цепочка из (N È T È A)^* и bàa Î P, aÎREG(N È T È A), a порождает d, то abgÞ_Gadg.

Описание правил с помощью РБНФ не расширяет определения грамматики. Можно показать, что любое правило, описанное с помощью РБНФ, можно заменить конечным множеством правил вида Bàb, bÎ(N È T È A)^* так, что язык, порождаемый грамматикой, не изменится.

4. ПРЕДСТАВЛЕНИЕ РЕГУЛЯРНЫХ ВЫРАЖЕНИЙ В ФОРМЕ СИНТАКСИЧЕСКИХ ДИАГРАММ

Правые части правил грамматики, описанных с помощью РБНФ, могут быть представлены в виде синтаксических диаграмм (далее диаграмм). Диаграмма представляет собой ориентированный граф, вершины которого будем называть состояниями, рёбра – переходами. Каждому переходу приписан один символ из алфавита N È T È A. Диаграмма имеет одно начальное состояние и непустое множество конечных состояний.

Формально синтаксическую диаграмму над алфавитом X определим как пятёрку

M = (N(M), S(M), F(M), E(M), R(M)),

где S(M) – множество состояний диаграммы, R(M) Í { ( i, j, a) | i, jÎ S(M), a Î X }. Тройка (i, j, a) - переход диаграммы из состояния i в состояние j с приписанным символом a. F(M) Î S(M) – начальное состояние диаграммы M, E(M) Í S(M) – множество конечных состояний диаграммы, N(M) – имя диаграммы. Заметим, что начальное состояние может являться конечным. В случае, когда нас не интересует значение какого-либо элемента тройки ( i, j, a )ÎR(M), на месте соответствующего элемента будем ставить точку. Например, запись ( i, . , . ) обозначает множество переходов, выходящих из состояния i Î S(M), ( . , j , a) – множество переходов с приписанным символом a Î X, входящих в состояние j Î S(M).

Построим конечный автомат K_M=(S, T, d, s₀, Q, m), соответствующий диаграмме M над алфавитом X:

- S = S(M) È {$ERROR};

- T = X;

- d(s,t)= { s’ | (s, s’, t)ÎR(M)}, если { s’ | (s, s’, t)ÎR(M)} ¹ Æ;

- d(s,t)= {$ERROR}, если { s’ | (s, s’, t)ÎR(M)} = Æ;

- s₀ = F(M);

- Q = {$END};

- m($END) = E(M).

Будем говорить, что синтаксическая диаграмма M порождает цепочку t, если

(s₀, t) ®_Km^* (s₁, e), s₁ Î m($END).

Языком L(M), порождаемым диаграммой M, будем называть множество цепочек, порождаемых диаграммой M. Говоря об эквивалентности регулярного выражения и диаграммы, будем иметь в виду равенство множеств цепочек, порождаемых регулярным выражением и диаграммой.

Графически диаграммы будем изображать в виде диаграммы состояния конечного автомата K, построенного выше. Вершины с маркером $END заштрихованы. Пример синтаксической диаграммы и правила РБНФ с эквивалентной ей правой частью приведён на рис. 1.

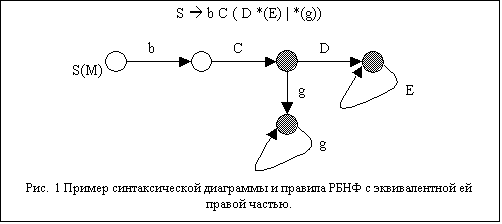
Каждому rÎREG(X) соответствует эквивалентная синтаксическая диаграмма, построенная по следующим рекурсивным правилам:

· для выражения a, aÎX построить диаграмму M: S(M) := {0,1}, E(M):={1}, F(M):=0, R(M):={(0, 1, a)};

· для выражения a b, aÎREG(X), bÎREG(X), для a построена диаграмма A, для b – B, диаграмма M строится следующим образом:

- переименовать элементы S(B) (и, соответственно, изменить R(B), E(B), F(B)) таким образом, что S(A) Ç S(B) = Æ ;

- S(M) := S(A) È S(B) ;

- F(M) := F(A) ;

- E(M) := E(B) ;

- если F(B)ÎE(B), то E(M):= E(M) È {E(A)};

- R(M) := Æ ;

- "qÎX: ( i, j, q)ÎR(M) : iÎS(A), jÎE(A), ( j, . , .) = Æ заменить на ( i, F(B), q);

- построить D = { iÎS(M) | i¹F(M) и ((., i, .)ÎR(M)) = Æ };

- S(M) := S(M) \ D;

- E(M) := E(M) \ D;

- построить Q = { ( j , q ) | (F(B), j, q)ÎR(B) };

- "iÎE(A), (i,. , .)ÎR(A) ¹ Æ , "( j , q )ÎQ: R(M) := R(M) È ( i, j, q);

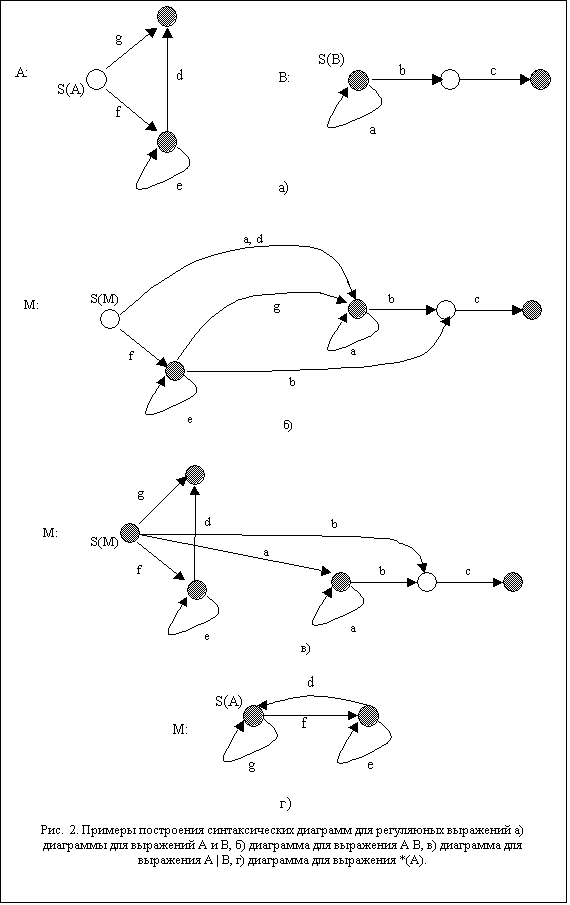
Пример построенной синтаксической диаграммы на рис. 2б;

· для выражения ( a | b ), a Î REG(X), b Î REG(X), для a построена диаграмма A, для b – B, используется следующий алгоритм построения диаграммы М:

- переименовать элементы S(B) (и, соответственно, изменить R(B), E(B), F(B)) таким образом, что S(A) Ç S(B) = Æ ;

- S(M) := S(A) È S(B) ;

- F(M) := F(A);

- E(M) := E(A) È E(B);

- если S(B)ÎE(B), то E(M) := E(M) È S(A)

- R(M) := Æ;

- построить Q = { (j, q) | (F(B), j, q)ÎR(B) };

- "( j , q )ÎQ: R(M) := R(M) È ( F(A), j, q);

- если ( ., F(B), .)ÎR(M) = Æ,

то S(M):=S(M) \ F(B),

E(M):=E(M) \ F(B),

R(M) := R(M) \ ( F(B) , . , . ).

Пример построенной синтаксической диаграммы на рис. 2в;

· для выражения *( a ), a Î REG(X), для a построена диаграмма A, используется следующий алгоритм построения диаграммы M:

- M := A;

- " iÎ E(M), i ¹ F(M):

если (( i, . , .) Í R(M)) ¹ Æ ,

то " (F(M), j, q)ÎR(M) R(M):=R(M) È ( i, j, q ),

иначе заменить все ( j, i, q)ÎR(M) на ( j, F(M), q), удалить i из множеств S(M) и E(M);

- E(M) := E(M) È {F(M)};

Пример построенной синтаксической диаграммы на рис. 2г;

· для выражения ?( a ), a Î REG(X), для a построена диаграмма A, используется следующий алгоритм построения диаграммы M:

- M := A;

- E(M) := E(M) È {F(M)};

· для выражения +( a ), a Î REG(X) синтаксическая диаграмма строится так же, как для *(a).a.

В программной реализации алгоритма построения диаграммы, эквивалентной регулярному выражению, регулярное выражение может быть представлено в виде дерева, листья которого – символы алфавита X, остальные узлы – метасимволы ‘*’, ’+’, ‘.’, ‘|’. Каждый узел соответствует регулярному выражению. Построение диаграммы начинается от листьев. На каждом шаге выбирается узел, для потомков которого уже построены диаграммы, и выполняется построение диаграммы для этого узла по вышеперечисленным правилам.

5. ОПРЕДЕЛЕНИЕ РАСПОЗНАВАТЕЛЯ

Определим распознаватель как пятёрку H=(T, N, A, D, d_S), где T – терминальный алфавит, N – диаграммный алфавит (его элементы – имена диаграмм множества D), A – алфавит СД, D – непустое конечное множество диаграмм, d_SÎD – начальная диаграмма.

Пусть G(N, T, A, P, S) – грамматика. Построим распознаватель для грамматики G следующим образом:

- множества T, N, A распознавателя являются соответственно множествами терминалов, нетерминалов и символов действия грамматики G;

- D – множество диаграмм, построенных для правых частей правил грамматики (предполагается, что левые части правил различны). Имя каждой диаграммы совпадает с нетерминалом, стоящего в левой части правила. Диаграмму с именем nÎN будем обозначать d_n;

- d_S – диаграмма c именем S.

Состояние распознавателя - двойка (d, s), где dÎD, sÎS(d). Множество всех состояний распознавателя H обозначим DS(H)={(d,s) | dÎD, sÎS(d)}.

Конфигурация распознавателя – четвёрка ((d , s), t$, w$), где (d , s) – состояние распознавателя, t - входная цепочка терминальных символов, w - стек состояний распознавателя (строка двоек (d,s)). $ - специальный символ, обозначающий конец строки. C(H) - множество всех конфигураций распознавателя H.

Переход распознавателя – тройка ((d₁,s₁), (d₂,d₂), c), где (d₁,s₁) и (d₂,s₂) – состояния распознавателя, cÎ{$PUSH, $POP} È T È A. Множество переходов R(H) распознавателя H=(T, N, A, D, d_S) определим следующим образом.

1. Если (i, j, a)ÎR(d), aÏN, dÎD то ((d, i), (d,j), a)ÎR(H).

2. Если (i, j, a)ÎR(d), aÎN, dÎD то

((d, i), (d_a,S(d_a), $PUSH)ÎR(H),

"kÎE(d_a): ((d_a, k), (d, j), $POP)ÎR(H).

Аналогично обозначению для переходов диаграммы, символ ‘.’, стоящий на месте какого-либо элемента перехода, будет обозначать применение квантора общности для этого элемента. Например, ((d,.),.,.) обозначает множество переходов {((d,s₁), (d₂,s₂), a) | "s1ÎS(d), "d2ÎD, "s₂ÎS(d₂), "aÎTÈAÈ{$PUSH, $POP}, ((d,s₁), (d₂,s₂), a)ÎR(H)}. Такое обозначение будем использовать, когда понятно, о каком распознавателе H идёт речь.

Графически распознаватель будем изображать как множество диаграмм. Переходы в пределах одной диаграммы изображаются сплошными стрелками, переходы между диаграммами – пунктирными. Символы cÎ{$PUSH, $POP} È T È A перехода приписываются к соответствующей стрелке. Когда необходимо, будем обозначать переходы выражениями вида [r_i], приписанными стрелке.

Будем называть распознаватель H детерминированным, если для каждого его состояния (d,s) определена функция

f_(d,s)(t) ® ((d,s),.,.) È {$ERROR},

указывающая либо один из переходов распознавателя, либо сигнал об ошибке, в зависимости от его состояния и входной строки t.

Работа детерминированного распознавателя состоит из конечной последовательности тактов. В каждый момент времени имеется одна т.н. текущая конфигурация c₀ÎC(H) распознавателя. Такт работы распознавателя заключается в изменении его текущей конфигурации или остановке работы. Новая текущая конфигурация определяется с помощью функции ®, которую определим как отношение на множестве C(H) È {$ERROR}:

(1) ((d,s), t$, w$) ® ((d,s₁) , t$, w$), если f_(d,s)(t) = ((d,s), (d,s₁), a) и aÎA;

(2) ((d,s), tt$, w$) ® ((d, s₁), t$, w$), если f_(d,s)(t) = ((d,s), (d,s₁), a) и aÎT;

(3) ((d,s), t$, w$) ® ((d₁, s₁), t$, (d,s)w$), если f_(d,s)(t) = ((d,s), (d₁,s₁), a) и a=$PUSH;

(4) ((d,s), t$, (d₀,s₀)w$) ® ((d₀,s₀), t$, (d,s)w$), если f_(d,s)(t) = ((d,s), (d₁,s₁), a) и a=$POP;

(5) ((d,s), t$, w$) ® $ERROR, если f_(d,s)(t) = $ERROR.

Очевидно, что отношение ® является функцией, т.к. A Ç T = Æ, $PUSH, $POP, $ERROR не принадлежат A È T. Если при выполнении очередного такта c₀®$ERROR, то работа распознавателя останавливается. Если значение ® было определено по правилу (1), то выполняется процедура, соответствующая символу действия aÎA (предполагается, что выполнение процедур, соответствующих СД, не влияет на работу распознавателя).

Обозначим ®^* рефлексивное и транзитивное замыкание отношения ®.

Будем говорить, что распознаватель H=(T, N, A, D, d_S) допускает строку t, если ((d_S,F(d_S)),t$,$)®^*((d_S,j),$,$), jÎE(d_S), иначе распознаватель отвергает строку t.

Будем говорить, что распознаватель распознаёт язык L, если он допускает все строки tÎL и отвергает строки tÏL.

Очевидно, что мощность множества распознаваемых распознавателем языков зависит от алгоритмов вычисления функций f_(d,s)(t).

6. SLL¹(K) ГРАММАТИКИ

Пусть (d,s)ÎDS(H) – состояние распознавателя H=(T, N, A, D, d_S), r Î ((d,s),.,.) – переход распознавателя H.

Определим множества FIRST_k(r) и FIRST_kⁱ(r), i=1…k:

FIRST_k(r)={ t_1…k | tÎT^*, $aÎDS(H)^*, f_(d,s)(t) = r, ((d,s),t$, a$)®^*((d_S, j), $, $), jÎE(d_S)},

FIRST_kⁱ(r)={ (a)_i | aÎFIRST_k(r)}, i=1…k.

Грамматика G, для которой построен распознаватель H, является SLL¹(k), если:

"(d,s)ÎDS(H): "r₁Î((d,s),.,.),"r₂Î((d,s),.,.), r₁ ¹ r₂,$iÎ[1,k], FIRST_kⁱ(r₁) Ç FIRST_kⁱ(r₂)=Æ.

Для сравнения приведём определение SLL(k) грамматики: грамматика G, для которой построен распознаватель H, является SLL(k), если:

"(d,s)ÎDS(H): "r₁Î((d,s),.,.),"r₂Î((d,s),.,.), r₁ ¹ r₂, FIRST_k(r₁) Ç FIRST_k(r₂)=Æ.

Говоря неформально, грамматика является SLL¹(k), если распознаватель, находясь в любом состоянии, всегда может выбрать единственный из альтернативных переходов, анализируя первые k символов входной цепочки и имея информацию о том, какие символы могут встретиться на i-й позиции, 1 £ i £ k, при выборе каждого перехода. Существенно то, что во время разбора для каждого перехода r известны лишь множества символов FIRST_kⁱ(r) на следующих позициях, а не строки – префиксы FIRST_k(r). В этом состоит отличие SLL¹(k) грамматик от SLL(k), распознаватель для которых во время разбора использует множества FIRST_k(r).

Как будет показано ниже, для вычисления и хранения множеств FIRST_kⁱ(r) требуется время и объём памяти, линейно зависящие от k и количества терминалов грамматики - |T|. Для хранения же множеств FIRST_k(r) требуется O(|T|^k) единиц памяти, поэтому на практике обычно не используются SLL(k) распознаватели при k>1.

Приведём пример SLL¹(k) – грамматики:

S à A b c

S à a c c

S à b B d

A à a | c

B à a | b | c

T={a, b, c}, N={A, B, S}, S – главный символ грамматики. Распознаватель изображён на рис. 3.

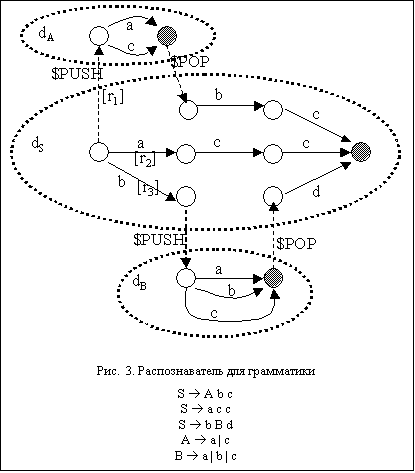
Данная грамматика является SLL¹(2).

Множества FIRST₂ⁱ(r) для переходов из состояния (d_S, 0) приведены в табл. 1.

r	FIRST2^1(r )	FIRST2^2(r )
r1	a, c	b
r2	a	c
r3	b	a, b, c

Таблица 1.

Находясь в состоянии (d_S,0), распознаватель всегда может выбрать из переходов r1, r2, r3 единственный, просмотрев первые 2 символа входной цепочки.

Отличие SLL(k) – грамматик от SLL¹(k) демонстрирует следующий пример:

пример SLL(2) – грамматики, не являющейся SLL¹(2).

S à A c

S à B d

A à ( b c | a b )

B à ( a c | b b )

T={a,b,c}, N={S}, S – главный символ грамматики. Распознаватель изображён на рис. 4.

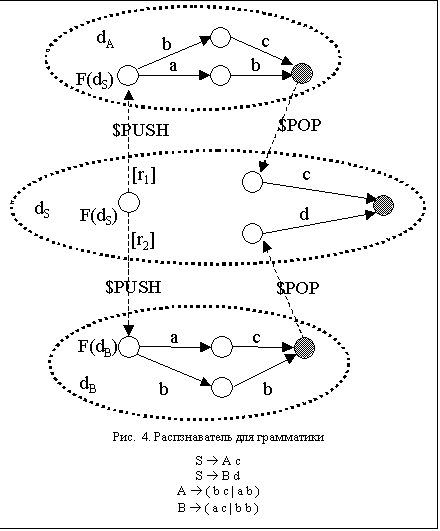
Множества FIRST₂ⁱ(r) для переходов из состояния (d_S, 0) приведены в табл. 2.

r	FIRST2^1(r )	FIRST2^2(r )
r1	a, b	c, b
r2	a, b	c, b

Таблица 2.

Множества FIRST₂(r) для переходов из состояния (d_S, 0):

FIRST₂(r1) = { bc, ab },

FIRST₂(r2) = { ac, bb }.

Очевидно, что множества FIRST₂ⁱ(r) не дают полезной информации для выбора перехода, поскольку они одинаковы для r1 и r2. Используя же множества FIRST₂(r), всегда можно выбрать единственный переход.

Для построения детерминированного распознавателя не всегда требуется хранить все множества FIRST_kⁱ(r). Ниже будет приведён алгоритм построения функций f_(d,s)(t) для каждого состояния SLL¹(k) - распознавателя.

7. АЛГОРИТМ ВЫЧИСЛЕНИЯ FIRST_K ⁱ (R), ОЦЕНКА ЕГО СЛОЖНОСТИ

Пусть имеется распознаватель H=(T, N, A, D, d_S). Требуется построить множества FIRST_kⁱ(r) для всех rÎR(H).

Введём вспомогательное множество XÍR(M).

1. X:=Æ, "rÎR(H): FIRST_kⁱ(r):=Æ;

2. для всех rÎ(.,(d_S, j),a), jÎE(d_S):

если aÎT, то

FIRST_k¹(r) := FIRST_k¹(r) È {a},

иначе

FIRST_k¹(r) := FIRST_k¹(r) È {$};

"i, 2 £ i £ k: FIRST_kⁱ(r) := FIRST_kⁱ(r) È {a},

X := X È {r};

3. если X=Æ, то закончить работу,

иначе выбрать r₀ = ((d₁,s₁), (d₂,s₂), a)ÎX, X:=X \ {r₀};

4. для всех rÎ(.,(d₁, s₁),a):

если aÎT, то

"i, 2£ i £ k: FIRST_kⁱ(r) := FIRST_kⁱ(r) È FIRST_k^i-1(r₀),

FIRST_k¹(r) := FIRST_k¹(r) È {a};

иначе

"i, 1£ i £ k: FIRST_kⁱ(r) := FIRST_kⁱ(r) È FIRST_kⁱ(r₀);

если FIRST_kⁱ(r) изменилось хотя бы для одного i, то X := X È {r};

5. перейти к шагу 3.

Покажем, что время выполнения алгоритма не превышает O(|T|*k*s*с), а требуемый объём памяти – O(|T|*k*s), где |T| - количество терминалов грамматики, k – константа, s – количество переходов распознавателя, c – максимальное количество переходов, входящих в одно и то же состояние.

Максимальное количество элементов каждого FIRST_kⁱ(r) составляет ровно |T|, суммарное количество элементов всех множеств FIRST_kⁱ(r), i=1…k для произвольного перехода rÎR(H) не превосходит k*|T|. Поскольку множество X содержит переходы распознавателя, то его мощность не превосходит s. Таким образом, для хранения всех множеств FIRST_kⁱ(r) и множества X требуется не более O(|T|*k*s) единиц памяти.

Шаги 1 и 2 алгоритма тривиальны и, очевидно, могут быть выполнены за время O(|T|*k*s).

Покажем, что шаги 3, 4 и 5 не могут быть выполнены более чем 2*|T|*k*s раз. Поскольку на шаге 4 переход r добавляется в множество X только в том случае, когда в FIRST_kⁱ(r) был добавлен новый элемент, то один и тот же r не может быть добавлен в X более k*|T| раз. Таким образом, на шаге 4 в множество X могут включаться новые элементы не более s*k*|T| раз, где s – количество переходов распознавателя. Возможен случай, когда после выполнения шага 2 X содержит все переходы rÎR(M). Поэтому шаг 4 может быть выполнен более 2*s*k*|T| раз.

В процессе выполнения шага 4 требуется просмотреть не более c переходов. Таким образом, общее время выполнения алгоритма не превышает O(|T|*k*s*c) единиц времени.

8. АЛГОРИТМ ПОСТРОЕНИЯ ФУНКЦИЙ F_(D,S)(t), ПРОВЕРКА НА ПРИНАДЛЕЖНОСТЬ ГРАММАТИКИ КЛАССУ SLL¹(K)

Пусть для каждого перехода rÎR(H) распознавателя H=(T, N, A, D, d_S) построены множества FIRST_kⁱ(r), i=1…k.

Построим конечный автомат K=(S, T_K, d, s₀, Q, m) для состояния (d,s)ÎDS(H). Обозначим {r_1,…r_N}– множество переходов из состояния (d,s), т.е {r₁,…r_N}=((d,s),.,.).

- S = { (i, r) | 1£ i £ k, rÎ{r_1,…r_N}} È {$FIRST, $ERROR};

- множество T_K конечного автомата совпадает с терминальным множеством T грамматики H;

- функцию переходов d определим так:

- для i=1…k-1, rÎ{r₁,…r_N}, tÎFIRST_kⁱ(r): d((i,r), t)= (i+1,r);

- для rÎ{r₁…r_N}, tÎFIRST_kⁱ(r): d($FIRST, t)= (1,r);

- во всех остальных случаях d( s,t )=$ERROR;

- s₀ = $FIRST;

- Q = {r₁,…r_N};

- m(r_i) = (k, r_i), i=1…N.

Пример конечного автомата приведён на рис. 5.

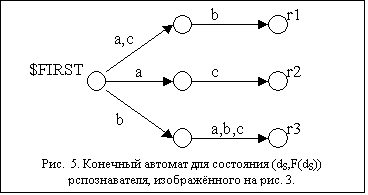
Построенный конечный автомат K был построен для произвольной грамматики. В общем случае он является недетерминированным. Опишем алгоритм построения детерминированного предсказывающего автомата.

Пусть K=(S, T_K, d, s₀, Q, m) – конечный автомат, построенный выше. Построим конечный автомат K₁=(S₁, T₁, d₁, s₀₁, Q₁, m₁) следующим образом:

- S₁ = Â(S) \ {Æ};

- T₁=T_k;

- функцию переходов d₁ определим так:

- если s={s₁,s₂,…,s_L}ÎS₁, то d₁(s, t) = { s’ | s’Îd(s_i, t), s_iÎs}ÎS₁;

- s₀₁ = {$FIRST};

- Q₁ = Â(Q) \ {Æ};

- "qÎQ₁: m(q) = { s | sÎS₁, "q’Îq: sÎm(q’), "q’’Ïq: sÏm(q’’) }.

Конечный автомат K₁ является детерминированным.

Пусть распознаватель имеет конфигурацию ((d, s), t$, w$). K₁ называется предсказывающим конечным автоматом, если "tÎT^* выполняется

либо ({$FIRST}, (t$)_1…k)®^*(s, e), |m₁^-1(s)| =1,

либо ({$FIRST}, (t$)_1…k)®^*({$ERROR}, a), aÎ(T È {$})^*.

В первом случае будем говорить, что K₁ предсказывает переход rÎm₁^-1(s), во втором – K₁ сообщает об ошибке. Для состояния (d,s) распознавателя положим f_(d,s)(t)= r, ({$FIRST}, (t$)_1…k) ®^* (r,e).

Процедура проверки грамматики G на принадлежность классу SLL¹(k) осуществляется следующим образом: строится распознаватель H, соответствующий грамматике G, затем для каждого состояния (d,s) распознавателя выполняется построение конечных автоматов K и K₁. Грамматика G является SLL¹(k), если K₁ является предсказывающим автоматом для всех состояний (d,s). Если грамматика является SLL¹(k), то одновременно с проверкой может быть построен детерминированный распознаватель, т.е. определены функции f_(d,s)(t).

На рис. 6 изображён предсказывающий автомат K₁, соответствующий автомату K, изображённому на рис. 5.

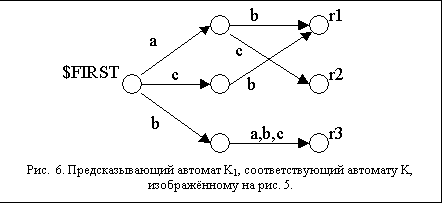
9. АЛГОРИТМ ФАКТОРИЗАЦИИ СИНТАКСИЧЕСКИХ ДИАГРАММ

На практике часто встречаются грамматики, правила которых могут быть упрощены с помощью процедуры факторизации, например, грамматика

S à a B

S à a b c

B à e

может быть преобразована в

S à a S1

S1 à B

S1 à b c

B à e.

Вторая грамматика является SLL¹(1), а первая – SLL¹(2), но не SLL¹(1). При использовании РБНФ для описания правил возможны и более сложные случаи:

S à *(a) ?(E) b | *(a) ?(E) | F E | F F

E à e

F à *(f)

можно преобразовать в

S à *(a) ?(E) ?(b) | F (E | F)

E à e

F à *(f).

Первая грамматика не является SLL₁(k) ни для какого k, преобразованная является SLL¹(2).

Алгоритм факторизации синтаксических диаграмм осуществляет преобразования диаграмм, построенных для правых частей правил грамматики, подобные показанным в примерах. Это позволяет в некоторых случаях упростить грамматику и построить для неё SLL¹(k) распознаватель. Факторизация диаграмм осуществляется до процедуры проверки грамматики на принадлежность классу SLL¹(k) и построения распознавателя. Опишем алгоритм факторизации диаграмм.

Пусть M = (N(M), S(M), F(M), E(M), R(M)) – синтаксическая диаграмма над алфавитом X, K_M=(S, T, d, s₀, Q, m) – конечный автомат, построенный для диаграммы M в пункте 2.

Состояния s₁ÎS(M) и s₁ÎS(M) являются эквивалентными (обозначается s1 « s2), если "tÎX^* выполняется:

(F(M),t) ®_Km^* (s₁,e) => (F(M),t) ®_Km^* (s₂,e),

(F(M),t) ®_Km^* (s₂,e) => (F(M),t) ®_Km^* (s₁,e).

Нетрудно убедиться, что отношение « является отношением эквивалентности на множестве S(M).

Наличие эквивалентных состояний в диаграммах распознавателя может усложнить или сделать невозможным построение детерминированного распознавателя.

Алгоритм факторизации диаграммы состоит в объединении эквивалентных состояний, т.е. построении диаграммы, состояниями которой являются классы эквивалентности отношения «.

Обозначим p₁ … p_k, p_iÎÂ(S(M)) – классы эквивалентности отношения «, обозначим

p_i,a = { sÎS(M) | $ jÎp _i, (s, j, a )ÎR(M)}.

Алгоритм построения классов эквивалентности p₁ … p _k:

1. p₁ = {F(M)}, p₂ = S(M) \ {F(M)}, k=2;

2. выбрать p_i, p_j, aÎX, такие, что p_i,a Ç p_j ¹ Æ. Если таких p_i, p_j и a нет, то конец работы алгоритма, p₁ …p_k – классы эквивалентности отношения «.

3. построить p_k+1 = { sÎp_j | j Ï p_i,a};

4. p_j := p_j \ p_i,a;

5. k := k+1;

6. перейти к шагу 2.

После построения p₁ … p_k построим диаграмму M' = (N(M'), S(M'), F(M'), E(M'), R(M')), где

N(M') – имя диаграммы M',

S(M') = {p₁, … p_k },

F(M') = p₁,

E(M') = { p_i | $sÎS(M), sÎp_i, sÎE(M) },

R(M') = { (p_p, p_q, a)Î R(M') | $(i, j, a) Î R(M), iÎp_p, jÎp_q}.

Нетрудно показать, что L(M) = L(M').

10. ЗАКЛЮЧЕНИЕ

Описанные в статье алгоритмы реализованы в программном комплексе Unisan, разработанном в Гомельском государственном университете. В настоящее время Unisan используется для разработки универсального транслятора языка ассемблера, настраиваемого на целевую платформу, для разбора языка тестовых воздействий в системе высокоуровневого проектирования цифровых устройств HLCCAD, для разбора выражений языка С в калькуляторе, встроенном в среду отладки программного обеспечения встроенных систем WInter и других проектах. Обновляемую информацию и демонстрационную версию Unisan можно получить по адресу http://newit.gsu.unibel.by. В таблице 3 приведены результаты сравнения наиболее распространенных генераторов распознавателей и Unisan.

Критерий сравнения	Unisan 2.45	Lex, Yacc (Flex 2.5, Bison 1.25)	Antlr 2.7.0
класс грамматик для синтаксического анализатора	SLL^1(k) + алгоритм факторизации	LALR(1)	SLL^1(k)
класс грамматик для лексического анализатора	регулярные	регулярные	SLL^1(k)
механизм работы	генерация бинарного файла с описанием грамматики	генерация исходного кода	генерация исходного кода
необходимость включать в проект дополнительные модули при компиляции сгенерированного кода	нет	нет	да
платформа, на которой работает генератор распознавателей	Win32	может быть портирован на любую, для которой имеется компилятор ANSI C	любая, требуется наличие JVM[1]^)
платформа, на которой может быть реализована внешняя программа	Win32	любая	любая
язык, на котором может быть реализована внешняя программа	С++, Object Pascal или другой, позволяющий работать с COM-интерфейсами	С, С++	C++, Java
возможность вставки исходного кода в описание грамматики	да	да	да
функции для создания препроцессора	да	нет	нет
встроенные функции для построения синтаксического дерева	да	нет	да
описание правил лексики	РБНФ	БНФ и регулярные выражения	РБНФ
описание правил синтаксиса	РБНФ	БНФ	РБНФ
время разбора тестового файла (5 Мбайт)	2,89 сек	0,98 сек	11,32 сек

Таблица 3.

СПИСОК ЛИТЕРАТУРЫ

1. Ахо А., Ульман Дж. “Теория синтаксического анализа, перевода и компиляции” М., Мир, 1978, т.1,2.

2. Грис Д. "Конструирование компиляторов для цифровых вычислительных машин" М.,Мир 1976.

3. Ф. Льюис,Д.Розенкранц, Р. Стирнз "Теоретические основы проектирования компиляторов" М., Мир, 1976.

4. Terence J. Parr "Obtaining Practical Variants of LL(k) and LR(k) for k>1 by Splitting the Atomic k-Tuple" PhD thesis, Purdue University, West Lafayette, Indiana, August 1993.

5. Terence Parr, Quong Russell "LL and LR Translaror Need k Tokens of Lookahead" Appeared in SIGPLAN Notices Volume 31 #2 February 1996.

6. Гомозов А.Л., Станевичене Л.А. Об одном обобщении регулярных выражений // Программирование. 2000. №5. С. 31-43.

7. Толкачёв А.И. Универсальный синтаксический анализатор // Материалы XXVI научной конференции по естественным, техническим и гуманитарным наукам. Гомель. 1997. С. 27-28.

8. Толкачёв А.И. Универсальный синтаксический анализатор и построение компиляторов на его основе // Новые компьютерные технологии в науке, технике, производстве и индустрии развлечений, Материалы республиканской научно-технической конференции, 9-13 марта 1998г. ГГУ им. Ф. Скорины.

9. Толкачёв А.И. Универсальный синтаксический анализатор и примеры его апробации // Новые математические методы и компьютерные технологии в проектировании, производстве и научных исследованиях, Материалы II Республиканской научно-технической конференции студентов и аспирантов 15-20 марта 1999г.

10. Толкачёв А.И. Универсальный синтаксический анализатор // Творчество молодых ‘99 Cборник научных работ студентов и аспирантов Гомельского Государственного университета им. Ф. Скорины. Гомель, 1999, с.13-14.

11. Толкачёв А.И. Языки программирования и описания аппаратуры : универсальный синтаксический анализатор. // Труды международной конференции "Информационные технологии в бизнесе, образовании и науке" Минск, 1999

12. Толкачёв А.И. Разработка компилятора и отладчика языка Vhdl. // Новые математические методы и компьютерные технологии в проектировании, производстве и научных исследованиях, Материалы III Республиканской научной конференции студентов и аспирантов 13-18 марта 2000г.

13. Толкачёв А.И. Универсальный синтаксический анализатор. // Новые математические методы и компьютерные технологии в проектировании, производстве и научных исследованиях, Материалы IV Республиканской научной конференции студентов и аспирантов 19-22 марта 2001г.

---

[1] JVM (Java virtual machine) англ. – виртуальная машина Java.